Papyrus - TranslateTo Moving Body Rotations

We will use Event OnUpdate to tell us, periodically, when the object should change, so what we will do is upon startup, register the script for an update based on a variable set to a 1 second default:

float Property delay = 1.0 Auto

Event OnLoad()
RegisterForSingleUpdate(delay)
endEvent

Event OnUpdate()
;we fill this in as described below
endEvent

This registers the script for a single update. After that we have to re-register if we want OnUpdate to fire again...Now we should check that the object is actually 3D-loaded to prevent any execution issues. Then we must make a unit vector within the OnUpdate call, which is what our utility function DirectionToAngles expects:

if (!Is3DLoaded())
return
endIf

float pX = Game.GetPlayer().X - X
float pY = Game.GetPlayer().Y - Y
float pZ = Game.GetPlayer().Z + 128.0 - Z

float mag = Math.sqrt(pX*pX + pY*pY + pZ*pZ)
pX /= mag
pY /= mag
pZ /= mag

float[] angles = DirectionToAngles(pX,pY,pZ)

Finally we use TranslateTo to move the object, and register for the next periodic call

TranslateTo(X,Y,Z,angles[0],angles[1],angles[2],10.0)

RegisterForSingleUpdate(delay)

We will use the following utility function:

float[] function DirectionToAngles(float uX, float uY, float uZ)
float aZ = 0

if (uY != 0)
aZ = Math.atan(uX/uY)
elseif (uX < 0)
aZ = -aZ
endIf

if (uY < 0)
aZ += 180.0
endIf

float u2D = uX*uX + uY*uY

float vAngle = -(Math.abs(uZ)/uZ)*Math.acos(u2D/Math.sqrt(u2D))

float aX = vAngle * Math.Cos(aZ)
float aY = -vAngle * Math.Sin(aZ)

float[] xyz = new float[3]
xyz[0] = aX
xyz[1] = aY
xyz[2] = aZ

return xyz
endFunction

Aside - Building the DirectionToAngles function: The orientation of a body according to a direction vector can be expressed in terms of two rotations, call them θ and Ψ. The first is the simple case of transforming the axis along yaw (Z). Then we have two vectors along a plane. Since they are on the same plane, we are sure that the angle between them would be expressed in the same way that the angles would appear after a planar cut is performed to yield that particular plane from 3-space.

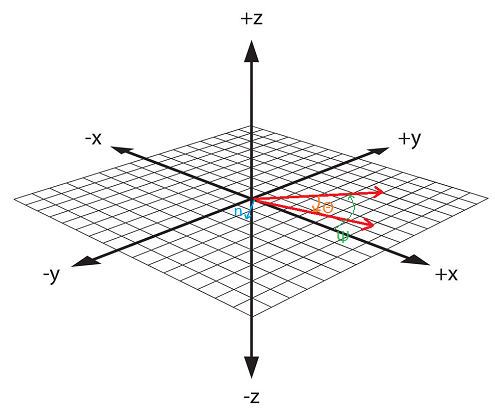
In other words, we are essentially looking once again at a 2-dimensional coordinate system. The angle between them can then be retrieved from the dot product formula: cos(a)*|u||v| = u.v; once we have these angles under local orientation, we have to transform the system to one that conforms to the universal axes, since Creation Engine uses extrinsic rotations. This involves extracting a formula from an X-Y rotation matrix.

So we have the full script below. Be sure to provide credit if used.

Scriptname TargetPointer extends ObjectReference  
;by EB/Xoleras, www.xoleras.com - please keep this here :)

int Property delay = 1 Auto
{how often the object changes to look at player}

Event OnLoad()
RegisterForSingleUpdate(delay)
endEvent

Event OnUpdate()

	if (!Is3DLoaded())
		return
	endIf

	float pX = Game.GetPlayer().X - X
	float pY = Game.GetPlayer().Y - Y
	float pZ = Game.GetPlayer().Z + 128.0 - Z

	float mag = Math.sqrt(pX*pX + pY*pY + pZ*pZ)

	pX /= mag
	pY /= mag
	pZ /= mag

	float[] angles = DirectionToAngles(pX,pY,pZ)

	TranslateTo(X,Y,Z,angles[0],angles[1],angles[2],10.0)

	RegisterForSingleUpdate(delay)

endEvent

float[] function DirectionToAngles(float uX, float uY, float uZ)
	float aZ = 0

	if (uY != 0)
		aZ = Math.atan(uX/uY)
	elseif (uX < 0)
		aZ = -aZ
	endIf

	if (uY < 0)
		aZ += 180.0
	endIf

	float u2D = (uX*uX + uY*uY)

	float vAngle = -(Math.abs(uZ)/uZ)*Math.acos(u2D/Math.sqrt(u2D))

	float aX = vAngle * Math.Cos(aZ)
	float aY = -vAngle * Math.Sin(aZ)

	float[] xyz = new float[3]
	xyz[0] = aX
	xyz[1] = aY
	xyz[2] = aZ

	return xyz
endFunction